Counting Up The Camels

Useful Magic (& Math) Tips

There are a few plot twists ahead — which is fitting, since puzzles often seem impossible.

As this month’s theme is “Out of the Box"—Meditation HERE—I’ve been researching the origin of that phrase.

Although its specific creator is unknown, it seems to derive from a particular puzzle, one that likely originated in the late 19th century.

The puzzle definitely appeared in IQ tests as early as the 1950s.

By the 1970s and 80s, it had become iconic through management consulting firms like McKinsey and various creativity workshops.

I’m speaking of the 9 dots puzzle.

The “Mission Impossible” challenge—should you choose to accept it:

Connect all 9 dots using exactly four straight lines,
without lifting your pen or retracing any line.

Go ahead and try… I’ll wait.

This week, I was also reminded of another classic puzzle — one I first heard in a meditation lecture.

In the parable, a farmer dies and leaves his 3 sons 17 cows.

Note: sometimes it’s camels, not cows—but the magic (and the math) remain the same.

The farmer’s will is very specific.

It dictates:

• The eldest son should receive ½ the cows

• The middle son ⅓

• The youngest ⅑

If they can’t do this, they inherit nothing.

Here’s the problem: you can’t really divide 17 cows (or camels) that way.

Half of 17 is 8.5. A third is 5.666... A ninth is 1.888...

You can’t split a cow (or camel) — at least, not lovingly.

So the sons argue, stuck with a real-world math problem that defies resolution, wondering if their inheritance can ever be claimed.

Last week I quoted the genius choreographer Twyla Tharp’s admonition that:

“Before you can think out of the box,
you have to start with a box”

Variations of a similar quote have been attributed to everyone from Picasso to Miles Davis to the Dalai Lama: “You must know the rules before you can break them.”

There’s value in constraint, in other words.

Indeed, in The Creative Habit, Twyla goes on to declare, writing about her experience with the New York City Ballet:

Whom the gods wish to destroy,
they give unlimited resources.

When she was invited to work with that prestigious company, she was given everything a choreographer could dream of: the best dancers, a great composer, a generous budget, and full artistic freedom.

Yet the experience was a creative disaster.

With no limitations, she had too many choices and no clear boundaries — and this overabundance diluted her focus.

Rather than fueling creativity, the vast freedom made her feel overwhelmed and directionless.

The resulting ballet was not well-received, and she came away with a powerful lesson:

(Sometimes) creative constraints are a gift.
Unlimited resources can paralyze.

Have you solved the 9 dots puzzle yet?

In a moment, I’ll reveal the classic solution.

But first, let me share why it’s iconic:

It shows us that creativity is often about questioning the box, not just working harder within it.

The box itself might be merely an assumption—an entirely self-imposed constraint.

And now, here’s the solution:

Note: you can only solve the puzzle if you allow yourself to draw quite literally “outside the box”

---

And what about those 17 cows / camels?

Taking a break from their squabbling, the brothers go to a wise elder (or sometimes a passing sage).

The elder thinks for a moment, then says:

“Let me lend you one of my cows/camels temporarily.”

(Sometimes the cow/camel is even imaginary).

Now the brothers have 18 camels to divide.

The math suddenly becomes easy.

• 1/2 of 18 = 9

• 1/3 of 18 = 6

• 1/9 of 18 = 2

That totals: 9 + 6 + 2 = 17

Each of the sons receives their fair share.

True, there’s one cow / camel left over (real or imaginary), but that’s not a problem since the elder simply takes it back (again, whether it’s real or imaginary).

The Lesson:

Sometimes, introducing a temporary or outside perspective — even something that doesn’t “exist” in the final outcome — is exactly what allows the impossible to resolve itself.

In other words, the solution can only be found by thinking outside the fixed constraints.

Otherwise you’re left with either nothing to inherit… or a brutally divided (and very messy) cow/camel situation.

Speaking of invisible dividers, I recently came across something fascinating about the Hermitage Museum in St. Petersburg (then Leningrad).

During World War II, the Hermitage even after evacuating its artworks for safekeeping, kept its doors open to the public.

Empty frames hung on the walls, accompanied by labels describing the missing pieces.

The museum itself had been bombed, and many staff lived in the freezing building during the siege, continuing their work with incredible dedication.

In fact, docents continued to give tours, vividly describing the absent artworks to visitors.

Beyond being a supremely brave act of cultural resilience — offering solace and a touch of normalcy amid the horrors of war — this points to something more.

It's one of the most poignant examples of how the frame can hold meaning, even when the painting is gone.

Indeed, according to eyewitness accounts, the absence of art didn’t dull the experience.

Instead, it highlighted the power of memory—and for those who had never seen the original paintings—imagination.

Sometimes, when the content transcends the box,
the box miraculously still holds what’s no longer inside.

Here’s the thing about the 9 dots puzzle.

The challenge was to solve it with four lines, which you can only do by going a little outside the box.

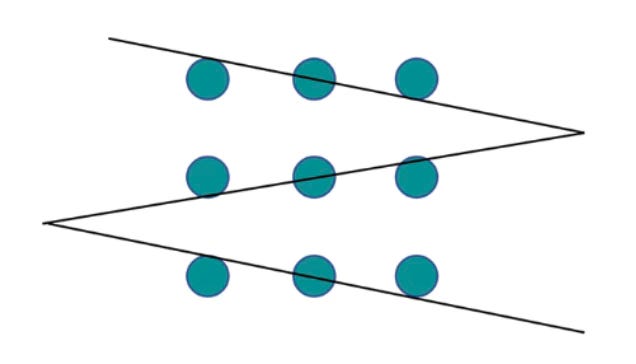
However, if you’re willing to REALLY go outside the box, you can actually do it in three lines.

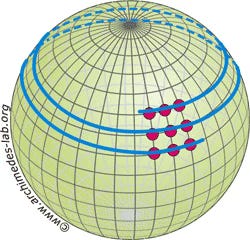
But wait … there’s an even more radical solution: one where you could connect all the dots with just one line.

You could simply fold the paper into a cylinder—or, conceived this way, imagine the dots positioned on a globe.

After all, the rules never insisted you work in only two dimensions.

Though Twyla Tharp wisely reminds us that great art often comes from tension, limits, and structure — not from boundless freedom — there’s incredible power in questioning the frame.

Sometimes it’s the lack — the constraint, the missing painting — that pushes us to see more clearly.

The most powerful solutions require us to go beyond the obvious borders — to question the limits we’ve unconsciously accepted.

Said another way:

The solution can’t arrive within the problem’s current limits.

Indeed, sometimes we need to go beyond thinking “outside the box” … and realize the box was never really there at all.

And sometimes, to solve an unsolvable math problem, an imaginary cow (or camel) is all you need.

Tell A New Story | Transform Your Life

June Meditation is HERE.

Work with me and Vlad 1:1 to Dissolve Your Boxes HERE.